Сайт преподавател И. Г. Пушкарёвой - Электронный учебник

СОДЕРЖАНИЕ

Тема 1.2. Гидростатика и гидродинамика

Вопросы:

1. Гидростатическое давление: определение, свойства, основное уравнение гидростатики

2. Закон Паскаля

3. Закон Архимеда

4. Основные понятия гидродинамики

5. Контрольные вопросы

Вопрос 1. Гидростатическое давление

Под гидростатическим давлением жидкости понимается давление, обусловленное действием только массовых сил, приложенных к частицам жидкости, находящейся в покое.

Гидростатическое давление обладает тремя свойствами:

1) гидростатическое давление всегда направлено по нормали к площадке, на которую оно действует;

2) гидростатическое давление в любой точке действует одинаково по всем направлениям;

3) гидростатическое давление в точке зависит от координат точки в пространстве, т. е. p = f (x, y, z).

Видео 1. Гидростатическое давление

Уравнение, определяющее гидростатическое давление в любой точке покоящейся жидкости (Видео 1), является основным уравнением гидростатики. Для его вывода рассмотрим равновесие жидкости, т. е. состояние, при котором на нее действует лишь одна массовая сила — сила тяжести G(вес).

Пусть в сосуде содержится жидкость (рис. 1) и на ее свободную поверхность действует внешнее давление р0. Ось системы координат направлена вертикально вверх, т. е. параллельно линии действия силы тяжести.

Рис. 1 Схема для вывода основного уравнения гидростатики

Найдем гидростатическое давление рв произвольной точке М, расположенной на глубине h от свободной горизонтальной поверхности. Возьмем около точки М элементарную площадку площадью и мысленно построим на ней прямоугольный параллелепипед с высотой h, а окружающую этот параллелепипед жидкость мысленно отбросим.

Чтобы не нарушить равновесие, приложим к параллелепипеду силы, заменяющие действие отброшенной части. Этими силами являются:

1) сила внешнего давления Fo, действующая по нормали к свободной поверхности; ее можно выразить через давление в виде

2) сила тяжести жидкости в параллелепипеде с площадью основании и высотой h, направленная вниз:

гдеV - объем жидкости в параллелепипеде;

3) сила гидростатического давления F, действующая снизу вверх на нижнее основание параллелепипеда:

где pабс - искомое абсолютное гидростатическое давление в точкеМ;

4)силы, действующие на боковую поверхность параллелепипеда; они взаимно уравновешиваются как равные по значению и противоположные по направлению.

Запишем условие равновесия рассматриваемого параллелепипеда относительно оси Oz

Сокращая это уравнение наполучаем основное уравнение гидростатики

Pабс= po+ pgh

Из этого уравнения следует, что абсолютное (или полное) гидростатическое давление Рабв в любой точке жидкости, находящейся в абсолютном покое, равно сумме внешнего давления и давления, вызванного силой тяжести столба жидкости, расположенной под рассматриваемой точкой.

Внешнеедавление р₀ может быть выше атмосферного (р_о>Р_атм) в закрытом сосуде и равным атмосферному (р₀ = р_атм) в открытом сосуде.

Положительную разность между абсолютным и атмосфернымдавлениями жидкости в открытом сосуде называют избыточнымдавлением (или манометрическим):

Ризб = Рабс - Ратм =rgh.

Напрактике для сокращения опускают слово «избыточное» перед словом «давление», подразумевая его.

Рис.2 Эпюры гидростатических давлений

Эпюры гидростатическогодавления для случаев ro>rатми ro=rатмпоказаны на рис. 2. Каждая ордината эпюры представляетсобойгидростатическое давление в соответствующей точке.Из эпюрыдавления наглядно видно, что избыточное давлениев любой точке жидкости зависит от глубины h ее погружения относительно свободной поверхности

Избыточное давление в открытом сосуде на поверхности жидкости равно нулю, а у дна сосуда rgH (где Н — глубина погружения дна сосуда).

Вопрос 2. Закон Паскаля

Закона Паскаля формулируется так: внешнее давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости и по всем направлениям одинаково.

Видео 2. Применение закона Паскаля в прессе

На законе Паскаля ( Видео 2) основаны принципы работы многих гидравлических машин и объемного гидропривода.

Рис.3. Схема работы простейшего гидропривода

Видео 3. Работа гидравлического домкрата

Простейшая схема гидропривода (Рис.3, Видео 3) состоит из двух гидромашин. Цилиндр 1 предназначен для работы в режиме насоса, цилиндр 2 - в режиме гидродвигателя (гидроцилиндра).

Принцип работы. При перемещении поршня цилиндра 1 вниз рабочая жидкость из него вытесняется в цилиндр 2, приводя его поршень в движение. При этом давление Р1, создаваемое в цилиндре 1 силой F1, действует также и на поршень цилиндра 2 (по закону Паскаля). В цилиндрах 1 и 2 устанавливается статическое давление, которое без учета потерь равно:

Р1 = F1/S1 = F2/S2 = Р2 = Р

Сила, действующая на поршень цилиндра 2:

F2 = РхS2 = F1хS2/S1

Сила F2 возрастает во столько раз, во сколько раз площадь большего поршня цилиндра 2 больше площади малого поршня цилиндра 1 без учета сил трения и разности масс поршней.

На законе Паскаля основан также принцип работы поступательного гидропреобразователя (гидравлического мультипликатора) - объемной гидромашины (Рис.4), предназначенной для преобразования энергии одного потока рабочей жидкости в энергию другого потока с изменением давления.

Рис.4. Схема поступательного гидропреобразователя

Видео 4. Закон Паскаля для газов

Вопрос 3. Закон Архимеда

Закон Архимеда - тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Видео

Изменение архимедовой силы

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) - центром водоизмещения.

При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O'-O", представляющей ось симметрии судна и называемой осью плавания (Рис.5).

Рис. 5. Поперечный профиль судна

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K'L'M', наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d'. Приложим к точке d' подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O'-O". Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным - в противном случае.

Рис.6. Живые сечения: а - трубы, б - клапана

Вопрос 4. Основные понятия гидродинамики

Смоченный периметр - часть периметра живого сечения, ограниченное твердыми стенками (рис.7, выделен утолщенной линией).

Рис.7. Смоченый периметр

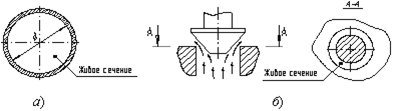
Расход потока (Q) - объем жидкости V, протекающей за единицу времени t через живое сечение .

Средняя скорость потока - скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения СОДЕРЖАНИЕ

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

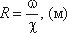
Гидравлический радиус потока R - отношение живого сечения к смоченному периметру

Линия тока - (применяется при неустановившемся движении) это кривая (Рис.8), в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока - трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис.8. Линия тока и струйка

Установившееся (стационарное) движение — это движение жидкости, неизменное во времени, т. е. такое движение, давление и скорость рассматриваемых точек которого зависит от координат точки, но не зависит от времени.

Неустановившееся (нестационарное) движение — это движение, при котором все параметры движущейся жидкости изменяются при изменении как координат точки, так и времени, т. е. var container = document.getElementById('nativeroll_video_cont'); if (container) { var parent = container.parentElement; if (parent) { const wrapper = document.createElement('div'); wrapper.classList.add('js-teasers-wrapper'); parent.insertBefore(wrapper, container.nextSibling); } }